Hybrid stepper motors (HSMs) are widely used in control systems because of their high positioning accuracy, compact size, and lower operation noise. Among various HSMs, the 3P-HSM has more advantages, such as higher torque and fewer MOSFETs in the control system, and thus, will dominate the HSMs market with the increase in market requirements in terms of motor performance and cost.
The optimization of HSMs is very difficult because of the complexity of the motor structure, the small air gap of the motor, and the presence of both axial and radial magnetic fields. The three-dimensional finite element method (FE method, FEM) is an effective tool for the analysis of such stepper motors, but they are extremely computationally intensive and require very long computation times, making them ineffective for the optimization of HSMs.
The 3P-HSM has a multi magnetic-pole structure and the most common structures include six-poles and 12-poles. Based on the unique electromagnetic (EM) structure of 3P-HSM, the reduction in motor torque ripple and noise has always been a research hotspot. The reduction is clearly related with the optimization of the motor design. It is clear that traditional optimization methods make it very difficult to carry out such an optimization calculation as a large number of FE calculations have to be used in the optimization process, and the required computation time is so long that optimization using FE calculations becomes infeasible. This paper presents the Taguchi method for the optimization of the EM structure of HSMs. The aim of the optimization is to reduce the torque ripple and operation noise of the motor. The Taguchi algorithm was proposed by Gen’chi Taguchi in the 1950s. Through local optimization, the Taguchi algorithm can establish the lowest FE model using the smallest number of tests, and use discrete data to find the best combination, which greatly reduces the time cost.
The sources of acoustic noise in the motor operation can be classified into three categories: mechanical, aerodynamic, and EM noise. In the 3P-HSM, the EM acoustic noise is mainly related to the drive circuit. The drive circuit noise is induced by the drive current with high-order harmonics. The drive current generates EM torque ripples, and then induces the vibration and acoustic noise in the motor’s operation. This noise type is not discussed here. This paper focuses on the EM noise caused by cogging torque ripples. Optimizing the motor tooth shape to reduce the THD is an effective method in terms of reducing motor cogging torque and improving motor noise. In order to minimize the THD, it is necessary to analyze and optimize the EM structure of 3P-HSM. Using a 3D FEM model, it is very difficult and time-consuming to carry out an EM analysis even for the 3P-HSM, let alone to optimize the motor. Taking the computation in the authors’ research on 3P-HSM as an example, it is known that one 3D FE mode needs about 1 million elements and 10 million nodes. For every “Torque-angle characteristic” curve, the torque for 30 rotor positions was calculated, and every FE computation needed about 2 h. Considering that four parameters needed to be optimized when using the FEM directly for the optimization, it is clear that it is not practical to use FEM directly for optimization calculations.
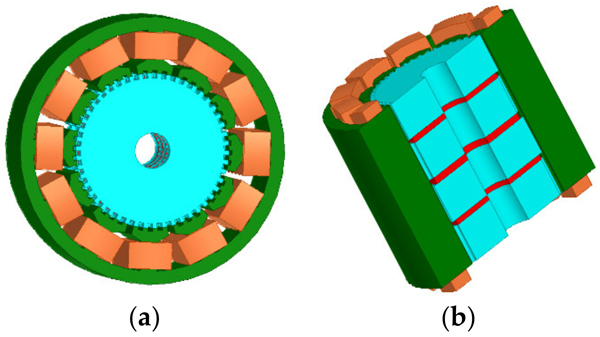
In this article, a method that combines the Taguchi method with FEM is introduced to optimize the tooth structure. This method can significantly reduce the results obtained via the FEM. A practical product for 3P-HSM is selected as the prototype for optimal design, which is shown in Figure 1. The optimization is aimed at reducing the THD of the holding torque. Furthermore, the testing results of the optimal THD-min 3P-HSM confirm the effectiveness of the optimization method.

Torque-Angle Characteristics
The torque-angle characteristics reflect the ability of the stepper motor to produce EM torque. Many researchers and engineers use the magnetic circuit method for calculations relating to motor design. Unlike the structure of other synchronous motors, the HSM has a more complex magnetic circuit, which contains both radial and axial magnetic paths. Figure 2 shows the equivalent magnetic circuit of the motor.

The energy of the HSM is mainly provided by the stator winding and permanent magnets. The energy dWe,n provided by the nth stator winding is as follows:
dWe,n = inNnd (φz,n) = Fz,nd (φzN,n + φzS,n)
where in is the stator winding’s current, Nn represents the stator winding’s turns, Fz,n is the stator winding’s magnetic potential, φz,n is the magnetic flux of the n-th pole stator’s teeth. Due to the adjacent rotor teeth differing by 1/2 tooth pitch, the magnetic field is divided into the N-side and the S-side. φzN,n and φzS,n are the tooth magnetic flux on the N-side and S-side, respectively.
The energy dWe,PM provided by the permanent magnet is shown:
dWe,PM = FPMφPM
where FPM and φPM are the magnetic potential and the magnetic flux of the permanent magnet, respectively.
The magnetic energy dWmag and the output mechanical energy dWmech can be expressed:
dWmag = 1/2d (φ2 / G)
where G is the magnetic permeance and φ is the magnetic flux of each part.
dWmech = Tdθ
where T is the torque and θ is the rotor rotation angle.
Considering the energy conservation, the torque can be obtained:
dWe = dWmag + dWmech
T = d / dθ (We,n + We,PM) – d / dθ (Wmag)
=1 / 2 * d / dθ (φ2PM / GPM)
where φvz is the stator’s axial yoke’s magnetic flux, and φaxz and φaxr represent the stator and rotor’s axial tooth’s leakage magnetic flux, respectively. φgzN,n and φgzS,n are the N-side and S-side’s stator radial inter-tooth’s leakage flux, φgN,n and φgN,n are the N-side and S-side’s air gap’s magnetic flux, φgrN,n and φgrS,n are the N-side and S-side’s rotor’s radial inter-tooth’s leakage flux, φrN,n and φrS,n are the N-side and S-side’s rotor’s radial inter-tooth’s magnetic flux, and φvr,N and φvr,S are the N-side and S-side’s rotor’s axial yoke’s magnetic flux.
In the actual optimization process, a slight change in the tooth structure has a great impact on the air gap’s magnetic field density. At the same time, the local magnetic saturation of HSMs must be considered. Therefore, the magnetic circuit method and FEM are often combined in the design of motors to improve the accuracy of the calculation results with regard to the torque-angle characteristics.
FEM Model of 3P-HSM
Due to its very complex EM structure and the large number of non-linear materials used in the motor, combined with the very small step angle, conventional methods, such as the equivalent magnetic circuit method, are unable to obtain highly accurate results for the analysis and calculation of HSMs. In recent years, designers have attempted to utilize 3D models to calculate the characteristic of stepper motors. Compared with other methods, FEM is better suited to the analysis and design of HSMs.
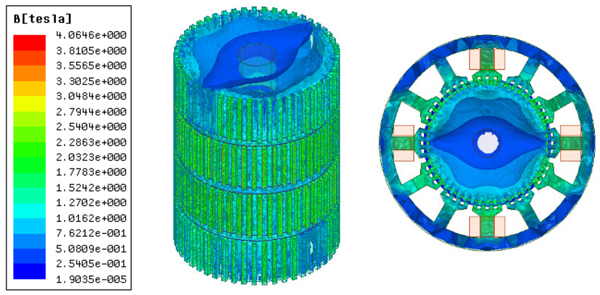
Figures 3 and 4 illustrate 3D models of the initial 3P-HSM and FEM mesh around the rotor teeth of the motor. The number of turns of the stator winding was 62. The magnetic density of the motor when 1.9A DC was applied to one-phase winding is shown in Figure 5. For HSMs, the tooth layer structure, which directly affects the tooth shape, is one of the main factors that determine the performance of the motor. In the calculations, high density meshes were used in the areas close to the iron small teeth; this, of course, significantly increased the computation time in the 3D-FEM calculation, in line with the findings given in [19]. In order to effectively utilize the results obtained from the 3D-FEM, the optimization of HSMs relies on the Taguchi optimization method, and this was also used in the authors’ research. The process will be presented in detail in the next section.

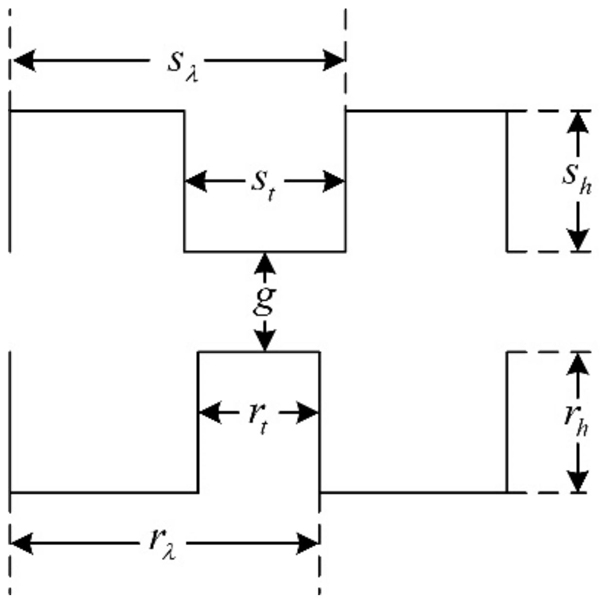
The main calculated parameters of the 3P-HSMs are listed in Tables 1 and 2. For HSMs, the tooth geometry is closely related with motor performance, and thus, was naturally selected for optimization.
In the past decades, researchers put forward different opinions about the tooth shape, such as it being rectangular, triangular, circular, and so on. Among them, the rectangular tooth shape shown in Figure 6 has been widely used in many products. However, according to practical experience, the trapezoidal tooth shape, as shown in Figure 7, is much better than the rectangular one, because this tooth profile contains more shape parameters and allows more degrees of freedom for optimization, making it easier to achieve the required motor performance.
| Parameters | Values |
| Stator poles | 12 |
| Small teeth stator pole | 4 |
| Rotor layers | 4 |
| Small teeth per rotor layer | 50 |
| Permanent magnets | 3 |
| Model | Tooth Geometry |
| Initial 3P-HSM | Rectangular |
| THD-min 3P-HSM | Trapezoidal |
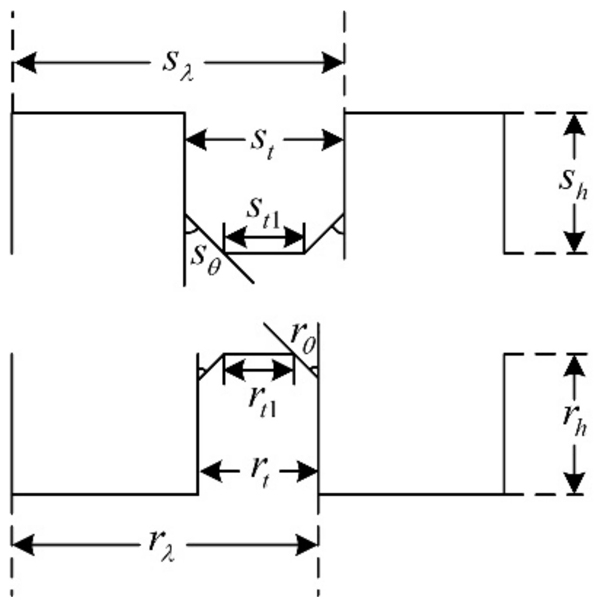
Optimization of 3P-HSM
In order to efficiently optimize HSMs with complex EM structures, an optimization approach combining FEM and the Taguchi optimization method was developed.
Taguchi Optimization Method
The Taguchi optimization algorithm, which is adept in the use of discrete results to identify the optimal point, has been widely used in many areas, e.g., national defense, chemical, and motor applications. The orthogonal array (OA) and the signal-to-noise(S/N) ratio are the main tools used in this method. The former was applied to design representative experiments and shorten the number of required hours. The latter was used to analyze the factors’ effect and determine the next optimization. Figure 8 shows the flowchart of the Taguchi optimization method.
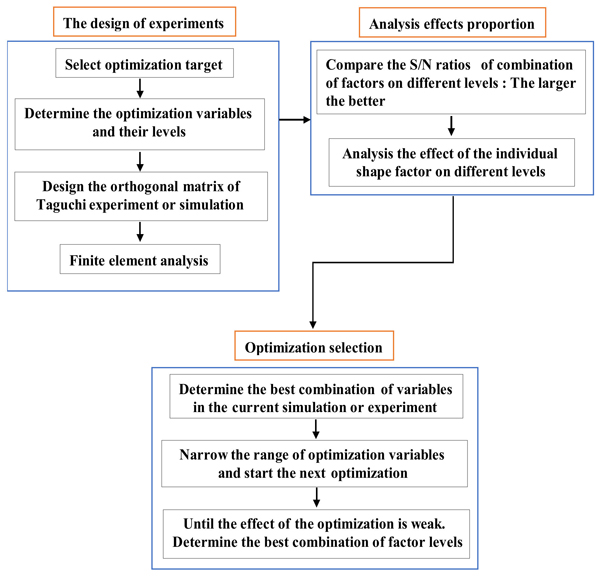
The Optimization Target: THD-min
In HSMs, the torque-angle characteristic is generally not sinusoidal and it is evidently affected by harmonics, especially the second ones, which will reduce motor performance and increase motor noise. In this study, it was desired to optimize the tooth geometry in order to reduce the harmonic.
The HSM with the original structure is defined as “Initial 3P-HSM”, and the motor with the optimized structure is denoted as “THD-min”. The optimization process of THD-min 3P-HSM was divided into two stages. The optimization parameters of each stage are shown in Table 3.
| Optimization Parameters | Optimization Stage | |
| First Stage | Second Stage | |
| A | rt1 / rλ | rt1 / rλ |
| B | st1 / sλ | st1 / sλ |
| C | rθ | rh / rλ |
| D | sθ | sh / sλ |
The combinations of signal-to-noise ratios, at different levels, for the four factors (A = rt1 / rλ, B = st1 / sλ, C = rθ, D = sθ) during the optimization process are shown in Table 4. The effect of each shape factor is reflected in Figure 9. It is clear that except that factor D had the least impact, the effect of each tooth shape factor was not significantly different. According to the average value of the S/N ratio, the best factor level combination can be judged as A1B3C4D3, where A1 = 0.15, B3 = 0.1, C4 = 15, and D3 = 60. After the first stage optimization, the THD of the THD-min 3P-HSM was reduced from 7.55% to 6.2% of the prototype’s initial 3P-HSM.
| NO. | Factor | THD (%) | S / N | |||
| A | B | C | D | |||
| 1 | 1 | 1 | 1 | 1 | 7.36 | – 17.34 |
| 2 | 1 | 2 | 2 | 2 | 7.10 | – 17.03 |
| 3 | 1 | 3 | 3 | 3 | 7.50 | – 17.50 |
| 4 | 1 | 4 | 4 | 4 | 7.91 | – 17.96 |
| 5 | 2 | 1 | 2 | 3 | 7.20 | – 17.15 |
| 6 | 2 | 2 | 1 | 4 | 7.30 | – 17.27 |
| 7 | 2 | 3 | 4 | 1 | 7.68 | – 17.71 |
| 8 | 2 | 4 | 3 | 2 | 8.10 | – 18.17 |
| 9 | 3 | 1 | 3 | 4 | 8.60 | – 18.69 |
| 10 | 3 | 2 | 4 | 3 | 8.51 | – 18.60 |
| 11 | 3 | 3 | 1 | 2 | 8.80 | – 18.89 |
| 12 | 3 | 4 | 2 | 1 | 9.81 | – 19.83 |
| 13 | 4 | 1 | 4 | 2 | 5.96 | – 15.50 |
| 14 | 4 | 2 | 3 | 1 | 6.80 | – 16.65 |
| 15 | 4 | 3 | 2 | 4 | 6.19 | – 15.83 |
| 16 | 4 | 4 | 1 | 3 | 7.00 | – 16.90 |
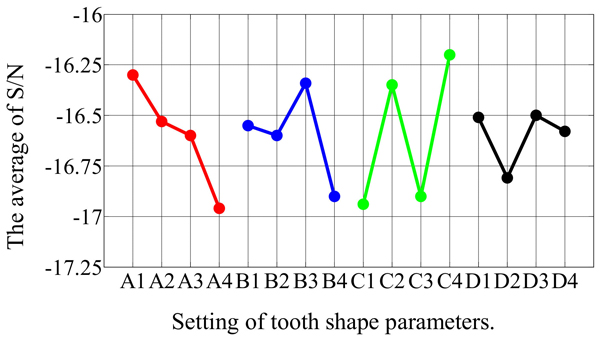
In the second stage of optimization, the impact of the parameters from the first stage was analyzed and the parameters for the new optimization were adjusted, as shown in Table 3. From Table 5 and Figure 10, the simulation results and the influence of the individual shape factors for the second stage, respectively, can be found. It is clear that A played a decisive role in the THD values, which were generally smaller when A was at level 4. The best combination of factor levels for the second stage was A4B1C4D2, where A4 = 0.45, B1 = 0.55, C4 = 0.2, and D2 = 0.6. Furthermore, the THD for the best combination of factor levels decreased from 6.2% to 5.96% in the first stage. Clearly, the second stage was relatively weak and, thus, the optimization was over at this stage.
| No. | THD (%) | S / N | ||||
| A | B | C | D | |||
| 1 | 1 | 1 | 1 | 1 | 6.54 | – 16.31 |
| 2 | 1 | 2 | 2 | 2 | 6.56 | – 16.34 |
| 3 | 1 | 3 | 3 | 3 | 6.20 | – 15.85 |
| 4 | 1 | 4 | 4 | 4 | 6.84 | – 16.70 |
| 5 | 2 | 1 | 2 | 2 | 6.80 | – 16.65 |
| 6 | 2 | 2 | 1 | 4 | 6.66 | – 16.47 |
| 7 | 2 | 3 | 4 | 1 | 6.20 | – 15.85 |
| 8 | 2 | 4 | 3 | 2 | 7.20 | – 17.15 |
| 9 | 3 | 1 | 3 | 4 | 7.00 | – 16.90 |
| 10 | 3 | 2 | 4 | 3 | 6.25 | – 15.92 |
| 11 | 3 | 3 | 1 | 2 | 7.43 | – 17.42 |
| 12 | 3 | 4 | 2 | 1 | 6.44 | – 16.18 |
| 13 | 4 | 1 | 4 | 2 | 6.56 | – 16.34 |
| 14 | 4 | 2 | 3 | 1 | 7.66 | – 17.68 |
| 15 | 4 | 3 | 2 | 4 | 6.48 | – 16.23 |
| 16 | 4 | 4 | 1 | 3 | 7.56 | – 17.57 |

The “torque-angle characteristic” of a hybrid stepper motor is closely related to the tooth shape of the motor. Optimization of the tooth shape of such motors is difficult because of the complexity of the motor structure, the small air gap of the motor, and the presence of both axial and radial magnetic fields. The three-dimensional finite element method is an effective tool for the analysis of such motors, but they are extremely computationally intensive and require very long computation times, making them ineffective for the optimization of hybrid stepper motors. In order to solve the problem of computational effort, an optimization method combining the FEM and Taguchi method is presented in this paper. The method was found to be able to make full use of the information from the FEM results to analyze and determine the direction of optimization with fewer discrete FE results, thus greatly reducing the number of times FEM needs to be undertaken in the optimization process and allowing the optimization to be implemented. This paper presents the results obtained using this method to optimize the tooth shape of a three-phase hybrid stepper motor with the objective of reducing the THD of the “torque-angle characteristic”. The performances of the motors with the original design and optimized design were analyzed. The new trapezoidal tooth shape reduced the THD of the “torque-angle characteristic” of the motor by 21% compared to the conventional rectangular tooth shape, which resulted in a significant improvement in motor noise. Therefore, the “FEM + Taguchi method” proposed in this paper is effective and can be used for the optimization of three-phase hybrid stepper motors, as well as for other types of motors.