The control system described in this article has been built specifically for driving a manipulator arm designed at the A.I. Lab by John Purbrick. This requires position control to within 1 mil and stab1e velocity control for speeds up to 3000 RPM. The manipulator has three rectilinear joints and three rotational joints, two of the latter driving a differential wrist. Two additional motors are provided to control a vise, which is part of the manipulator. Since this system is quite general in structure, it should lend itself to a fairly wide variety of stepping motor applications.
Several features of stepping motors make them attractive for this application. First, the discrete and repeatable nature of their motion makes precise positioning easy. Second, shaft encoders are available with outputs commensurate with the motor steps, facilitating the entire design. Third, in addition to being capable of high speeds, stepper motors can move very slowly without” stick-and-slip” problems. Fourth, the holding torque of the motors eliminates the need for brakes. Finally, open loop stepping provides a means of achieving smooth velocities without heavy dependence on velocity feedback, in particular, tachometers. The control system is designed around Superior Electric M Series stepping motors: The latter are 200 step / revolution 4 phase DC permanent magnet motors, with bifilar windings.
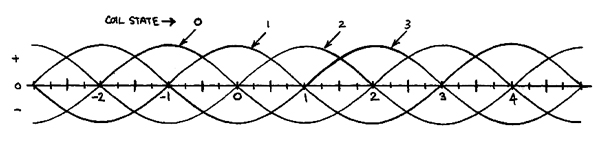
In this type of winding, the four coils are grouped into two pairs, the coils within a pair being tightly linked, inductively. The motors are used here as shown in fig. 1. One coil in each pair 15 always activated, resulting in four distinct states as shown below (coils are identified by lead color, referring to fig. 1.):

| Coil State | G | G / N | R | R / W |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 2 | 1 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 | 1 |
The arithmetic code on the left is used throughout the control system. An incrementing sequence of coil states (0, 1, 2, 3, 0, …) represents forward motion of the motor shaft. This in turn is defined as counter clockwise rotation,viewed from the motor label.
Associated with the four coil states are four static torque curves, which represent torque as a function of position for a given coil state, assuming a fixed rotor. Typical curves are shown in fig. 2 ( the position representation used in fig. 2 and 3 is explained in the next section ). Here as elsewhere in this paper, it is assumed that these curves are sinusoidal.
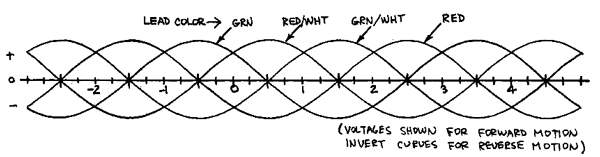
An important factor in this system is the back EMF generated by the motor itself. This quantity, a voltage, is also roughly a sine wave, with amplitude proportional to the (signed) angular velocity. Measured with respect to the center taps (see fig. 1), the voltages at the four end leads, for forward motion, are as shown 1n fig. 3.
Feedback
Position feedback is provided by pulse generating shaft encodes. These devices are mounted on each motor, and output two TTL square waves in quadrature as the shaft rotates. Each square wave has 200 cycles per shaft revolution. By virtue of the quadrature relationship, the two phases partition a complete shaft rotation into 800 segments. These occur as a repetitive sequence of the following encoder states:
| Encoder State | B Phase | A Phase |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 1 | 1 |
| 3 | 1 | 0 |
Both the arithmetic code and the gray code are used in the system. A single XOR gate suffices to convert between codes. Unless otherwise stated, it is the binary code that is referred to in this article. An incrementing sequence of encoder states (0, 1, 2, 3, 0, … – arithmetic code) represents forward motion.
It should be noted that the four encoder states – 0, 1, 2, 3 – constitute exactly one step. The encoders are aligned on the motor shafts so that the 1 – >2 encoder transition occurs at the rest or detent position of the motor.
this convention gives rise to a natural position representation, with the encoder state serving as the right most two bits, and an arbitrary number of bits to the left (14 in the case of this system), corresponding to the step. The step portion of the position is programmable, but the encoder state or quarter step portion is strictly dictated by the encoder. By convention we will assume that the detent position of coil state 0 corresponds to the 1->2 encoder transition of step 0. This must be effected by initialization.
The shaft encoders also output an index pulse, or mark, once per revolution. This is used for calibration of the manipulator during initialization.
Except for limit switches no other feedback is used in the stepper motor control system. In particular, there are currently no plans for using tachometers.
Phase angle and lead angle
In discussing stepper motors it very useful to have a simple terminology to describe the relationship between the coil state and the motor shaft. The concepts of phase angle and lead angle are introduced for this purpose. The phase angle is defined as the amount by which the coils are leading the shaft, or, more specifically, as the rightmost 4 bits of the quantity (PA) obtained by subtracting position (POS) from four times the coils state (CS):
PA = 4 * CS – POS (rightmost 4 bit)
The. multiplicative factor is necessary since a motor step consists of four encoder steps. This representation allows for 16 phase angles: 0, 1 through 7, -1 through -7, 8, and -8, the 1ast two being equal and ambiguous. Since the unit 1s a quarter step, we can represent phase angles up to +2 or -2 steps. Phase angles with magnitudes greater than 2 motor steps are equivalent to smaller phase angles, namely, those represented by the rightmost 4 bits. Phase angles are arbitrary in so much as the step portion of position is arbitrary, prior to initialization. In other words , even though it may seem reasonable to choose the detent position of step 0 as corresponding to coil state 0 at initialization, resulting in an initial phase angle of -1 or -2,it is an arbitrary choice. The phase angle, a periodic function of position and coil state, is always defined.
The lead angle is one of the two phase angles associated with the instant that” the motor coils are switched from one state to the next. In the case of forward motion, the phase angle after the coil transition is indicated. In the case of reverse motion, it is the phase angle before the transition. Negative lead angles are sometimes referred to as lag angles. Lead angles are discussed further in the next section.
Low level control
An important method for controlling stepping motors can now be introduced. This method will be ca1led lead angle control since it consists of imposing a fixed- lead angle (LA) upon: the motor. This amounts to solving the phase angle equation for coil state:
CS = (POS + LA) / 4 (rightmost 2 bits)
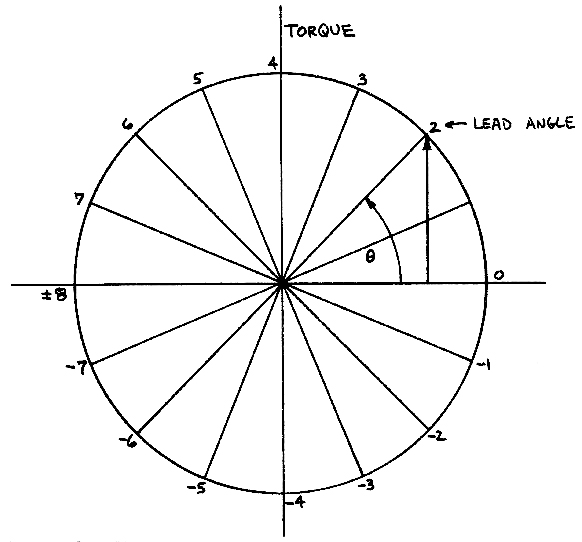
Static torque curves are also meaningful in reference to lead angles. In fig. 4 the static torque curve for LA = 5 is superimposed on those of the four coil states. Associated with each lead angle is an average static torque, proportional to the integral of a single period. These average static torques are sinusoidal as functions of lead angle. A circular representation, suggested by Matt Mason, is show in Fig. 5. The angle is equal to LA * π / 8; the y-axis represents torque. The static nature of this quantity must be emphasized. the average dynamic torque is a much more difficult quantity to derive, other than qualitatively. The main effects to consider are the delay time in turning one coil off and another on, and motor back EMF, which subtracts from the driving voltage. At even moderate speeds these factors significantly affect motor torque. The net result is contraction and rotation (clockwise for forward motion and counter clockwise for reverse motion) of the torque diagram. Both effects increase with motor speed. An important consequence of this is that lead angles with negative static torques can have positive dynamic torques at high speeds, and vice versa. Control schemes must take this effect into account.

Associated with the average dynamic torque is a terminal velocity. This is the velocity at which the average torque exactly compensates tor the losses due to friction and other effects. Assuming that the static torque associated with a lead angle is sufficient to start the rotor in motion in the right diction, the velocity will slew up to this value and stay there. Terminal velocities for one of the motors used here are plotted in fig. 6. Unfortunately, the terminal velocity corresponding to a particular lead angles, while providing a convenient way of slewing between velocities, do not constitute, in themselves, a means for stable velocity control. This does, not rule out stepper motor higher level control schemes, such as lead angle modulation, which Matt Mason has employed with considerable success. Fig. 7 shows phase angle plotted against time for a motor running at a terminal velocity, under lead angle control.


Probably the most common method of controlling stepper motors is the open loop method. This consists of stepping the coils at uniform intervals, determined by the desired step rate. The result, in general, is rotation of the motor shaft in the. direction of the coils. Unfortunately, this is not necessarily the case. First, the rotor may not be able to follow the coils at all, the result being stalling. Second, whereas the coils may be advancing forward at rate X,the rotor may actually move backward at rate 3X, or even forward at rate 5X. This is due to the existence of harmonics, as illustrated in fig. 9. They do not pose much of a problem, since the higher order harmonics are. increasingly unstable.
It is instructive to plot phase. angle vs. time for a motor running under open loop control. Some examples are shown in fig. 8. It can be seen from these that open loop control also results indirectly in a lead angle. Presumably these lead angles are precisely those required to achieve the open loop stepping rate as a terminal velocity, under lead angle control. At resonant frequencies the phase angle goes through more complicated gyrations.

