Small stepper motors, such as those used for head positioning on floppy disk drives, are usually driven at a low DC voltage, and the current through the motor windings is usually limited by the internal resistance of the winding. High torque motors, on the other hand, are frequently built with very low resistance windings; when driven by any reasonable supply voltage, these stepper motors typically require external current limiting circuitry.
There is good reason to run a stepper motor at a supply voltage above that needed to push the maximum rated current through the motor windings. Running a motor at higher voltages leads to a faster rise in the current through the windings when they are turned on, and this, in turn, leads to a higher cutoff speed for the motor and higher torques at speeds above the cutoff. Microstepping, where the control system positions the motor rotor between half steps, also requires external current limiting circuitry. For example, to position the rotor 1/4 of the way from one step to another, it might be necessary to run one motor winding at full current while the other is run at approximately 1/3 of that current.
The remainder of this section discusses various circuits for limiting the current through the windings of a stepper motor, starting with simple resistive limiters and moving up to choppers and other switching regulators. Most of these current limiters are appropriate for many other applications, including limiting the current through conventional DC motors and other inductive loads.
Resistive Current Limiters
The easiest to understand current limiter is a series resistor. Most motor manufacturers recommended this approach in their literature up until the early 1980’s, and most motor data sheets still give performance curves for motors driven by such circuits. The typical circuits used to control the current through one winding of a permanent magnet or hybrid motor are shown in Figure 1.

R1 in this figure limits the current through the motor winding. Given a rated current of I and a motor winding with a resistance Rw, Ohm’s law sets the maximum supply voltage as I (Rw + R1). Given that the inductance of the motor motor winding is Lw, the time constant for the motor winding will be Lw / (Rw + R1). Figure 2 illustrates the effect of increasing the resistance and the operating voltage on the rise and fall times of the current through one winding of a stepper motor.

R2 is shown only in the unipolar example in Figure 1 because it is particularly useful there. For a bipolar H-bridge drive, when all switches are turned off, current flows from ground to the motor supply through R1, so the current through the motor winding will decay quite quickly. In the unipolar case, R2 is necessary to equal this performance.
Note: When the switches in the H-bridge circuit shown in Figure 1 are opened, the direction of current flow through R1 will reverse almost instantaneously! If R1 has any inductance, for example, if it is wire-wound, it must either be bypassed with a capacitor to handle the voltage kick caused by this current reversal, or R2 must be added to the H-bridge.
Given the rated maximum current through each winding and the supply voltage, the resistance and wattage of R1 is easy to compute. R2 if it is included, poses more interesting problems. The resistance of R2 depends on the maximum voltage the switches can handle. For example, if the supply voltage is 24 volts, and the switches are rated at 75 volts, the drop across R2 can be as much as 51 volts without harming the transistors. Given an operating current of 1.5 amps, R2 can be a 34 ohm resistor. Note that an interesting alternative is to use a zener diode in place of R2.
Figuring the peak average power R2 must dissipate is a wonderful exercise in dynamics; the inductance of the motor windings is frequently undocumented and may vary with the rotor position.
The power dissipated in R2 also depends on the control system. The worst case occurs when the control system chops the power to one winding at a high enough frequency that the current through the motor winding is effectively constant; the maximum power is then a function of the duty cycle of the chopper and the ratios of the resistances in the circuit during the on and off phases of the chopper. Under normal operating conditions, the peak power dissipation will be significantly lower.
Linear Current Limiters
A pair of high wattage power resistors can cost more than a pair of power transistors plus a heat sink, particularly if forced air cooling is available. Furthermore, a transistorized constant current source, as shown in Figure 3, will give faster rise times through the motor windings than the current limiting resistor shown in Figure 1. This is because a current source will deliver the full supply voltage across the motor winding until the current reaches the rated current; only then will the current source drop the voltage.

In Figure 3, a transistorized current source (T1 plus R1) has been substituted for the current limiting resistor R1 used in the examples in Figure 1. The regulated voltage supplied to the base of T1 serves to regulate the voltage across the sense resistor R1, and this, in turn, maintains a constant current through R1 so long as any current is allowed to flow through the motor winding.
Typically, R1 will have as low a resistance as possible, in order to avoid the high cost of a power resistor. For example, if the forward voltage drops across the diode in series with the base T1 and VBE for T1 are both 0.65 volts, and if a 3.3 volt zener diode is used for a reference, the voltage across R1 will be maintained at about 2.0 volts, so if R1 is 2 ohms, this circuit will limit the current to 1 amp, and R1 must be able to handle 2 watts.
R3 in Figure 3 must be sized in terms of the current gain of T1 so that sufficient current flows through R1 and R3 to allow T1 to conduct the full rated motor current.
The transistor T1 used as a current regulator in Figure 3 is run in linear mode, and therefore, it must dissipate quite a bit of power. For example, if the motor windings have a resistance of 5 ohms and a rated current of 1 amp, and a 25 volt power supply is used, T1 plus R1 will dissipate, between them, 20 watts! The circuits discussed in the following sections avoid this waste of power while retaining the performance advantages of the circuit given here.
When an H-bridge bipolar drive is used with a resistive current limiter, as shown in Figure 1, the resistor R2 was not needed because current could flow backwards through R1. When a transistorized current limiter is used, current cannot flow backwards through T1, so a separate current path back to the positive supply must be provided to handle the decaying current through the motor windings when the switches are opened. R2 serves this purpose here, but a zener diode may be substituted to provide even faster turn-off.
The performance of a stepper motor run with a current limited power supply is noticeably better than the performance of the same motor run with a resistively limited supply, as illustrated in Figure 4:

With either a current limited supply or a resistive current limiter, the initial rate of increase of the current through the inductive motor winding when the power is turned on depends only on the inductance of the winding and the supply voltage. As the current increases, the voltage drop across a resistive current limiter will increase, dropping the voltage applied to the motor winding, and therefore, dropping the rate of increase of the current through the winding. As a result, the current will only approach the rated current of the motor winding asymptotically.
In contrast, with a pure current limiter, the current through the motor winding will increase almost linearly until the current limiter cuts in, allowing the current to reach the limit value quite quickly. In fact, the current rise is not linear, rather, the current rises asymptotically towards a limit established by the resistance of the motor winding and the resistance of the sense resistor in the current limiter.
This maximum is usually well above the rated current for the motor winding.
Open Loop Current Limiters
Both the resistive and the linear transistorized current limiters discussed above automatically limit the current through the motor winding, but at a considerable cost, in terms of wasted heat. There are two schemes that eliminate this expense, although at some risk because of the lack of feedback about the current through the motor.
Use of a Voltage Boost
If you plot the voltage across the motor winding as a function of time, assuming the use of a transistorized current limiter such as is illustrated in Figure 3, and assuming a 1 amp 5 ohm motor winding, the result will be something like that illustrated in Figure 5:
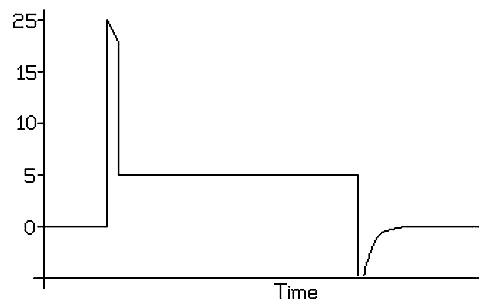
As long as the current is below the current limiter’s set point, almost the full supply voltage is applied across the motor winding. Once the current reaches the set point, the voltage across the motor winding falls to that needed to sustain the current at the set point, and when the switches open, the voltage reverses briefly as current flows through the diode network and R2.
An alternative way to get this voltage profile is to use a dual-voltage power supply, turning on the high voltage for as long as it takes to bring the current in the motor winding up to the rated current, and then turning off the high voltage and turning on the sustaining voltage. Some motor controllers do this directly, without monitoring the current through the motor windings. This provides excellent performance and minimizes power losses in the regulator, but it offers a dangerous temptation.
If the motor does not deliver enough torque, it is tempting to simply lengthen the high-voltage pulse at the time the motor winding is turned on. This will usually provide more torque, although saturation of the magnetic circuits frequently leads to less torque than might be expected, but the cost is high! The risk of boning out the motor is quite real, as is the risk of demagnetizing the motor rotor if it is turned against the imposed field while running hot. Therefore, if a dual-voltage supply is used, the temptation to raise the torque in this way should be avoided!
The problems with dual voltage supplies are particularly serious when the time intervals are under software control, because in this case, it is common for the software to be written by a programmer who is insufficiently aware of the physical and electrical characteristics of the control system.
Use of Pulse Width Modulation
Another alternative approach to controlling the current through the motor winding is to use a simple power supply controlled by pulse width modulation (PWM) or by a chopper. During the time the current through the motor winding is increasing, the stepper motor control system leaves the supply attached with a 100% duty cycle. Once the current is up to the full rated current, the control system changes the duty cycle to that required to maintain the current. Figure 6 illustrates this scheme:
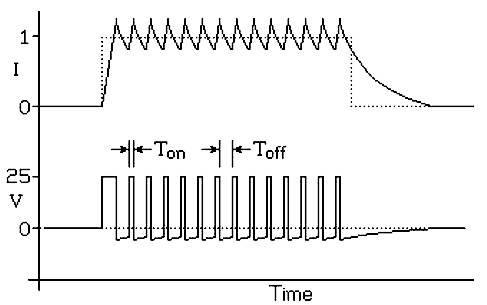
For any chopper or pulse width modulator, we can define the duty-cycle D as the fraction of each cycle that the switch is closed: D= Ton / (Ton + Toff)
Where
Ton – time the switch is closed during each cycle
Toff – time the switch is open during each cycle.
The voltage curve shown above indicates the fill supply voltage being applied to the motor winding during the on-phase of every chopper cycle, while when the chopper is off, a negative voltage is shown. This is the result of the forward voltage drop in the diodes that are used to shunt the current when the switches turn off, plus the external resistance used to speed the decay of the current through the motor winding.
For large values of Ton or Toff the exponential nature of the rise and fall of the current through the motor winding is significant, but for sufficiently small values, we can approximate these as linear.
Assuming that the chopper is working to maintain a current of I and that the amplitude is small, we will approximate the rates of rise and fall in the current in terms of the voltage across the motor winding when the switch is closed and when it is open: Von= Vsupply – I (Rwindng + Ron)
Voff = Vdiode + I (Rwinding + Roff) Here, we hump together all resistances in series with the winding and power supply in the on state as Rom and we lump together all resistances in the current recirculation path when the switch(es) are open as Roff. The forward voltage drops of any diodes in the current recirculation path have been lumped as Vdiode; if the off-state recirculation path runs from ground to the power supply (H-bridge fast decay mode), the supply voltage must also be included in Vdiode.
Forward voltage drops of any switches in the on-state and off-state paths should also be incorporated into these voltages.
To solve for the duty cycle, we first note that:
dI / dt = V / L
Where
I – current through the motor winding
V – voltage across the winding
L – inductance of the winding
We then substitute the specific voltages for each phase of operation:
Iripple / Toff = Voff / L
Iripple / Ton = Voff / L
Where
Iripple – the peak to peak ripple in the current
Solving for Toff and Ton and then substituting these into the definition of the duty cycle of the chopper, we get: D = Ton / (Ton + Toff) = Voff / (Von + Voff)
If the forward voltage drops in diodes and switches are negligible, and if the only significant resistance is that of the motor winding itself, this simplifies to: D = I Rwinding / Vsupply = Vrunning / Vsupply
This special case is particularly desirable because it delivers all of the power to the motor winding, with no losses in the regulation system, without regard for the difference between the supply voltage and the running voltage.
The AC ripple Iripple superimposed on the running current by a chopper can be a source of minor problems; at high frequencies, it can be a source of RF emissions, and at audio frequencies, it can be a source of annoying noise. For example, with audio frequency chopping, most stepper controlled systems will “squeel”, sometimes loudly, when the rotor is displaced from the equilibrium position.
To find the ripple amplitude, first recall that: Iripple / Toff = Voff / L. Then solve for Iripple: Iripple = Toff Voff / L.
Thus, to reduce the ripple amplitude at any particular duty cycle, it is necessary to increase the chopper frequency. This cannot be done without limit because switching losses increase with frequency. Note that this change has no significant effect on AC losses; the decrease in such losses due to decreased amplitude in the ripple is generally offset by the effect of increasing frequency. The primary problem with use of a simple chopping or pulse- width modulation control scheme is that it is completely open loop. Design of good chopper based control systems requires knowledge of stepper motor characteristics such as inductance that are frequently poorly documented, and as with dual-voltage supplies, when motor performance is marginal, it is very tempting to increase the duty-cycle without attention to the long-term effects of this on the motor. In the designs that follow, this weakness will be addressed by introducing feedback loops into the low level drive system to directly monitor the current and determine the duty cycle.
One – Shot Feedback Current Limiting
The most common approach to automatically adjusting the duty cycle of the switches in the stepper driver involves monitoring the current to the motor windings; when it rises too high, the winding is turned off for a fixed interval. This requires a current sensing system and a one-shot, as illustrated in Figure 7:

Figure 7 illustrates a unipolar drive system. As with the circuit given in Figure 3, R1 should be as small as possible, limited only by the requirement that the sense voltage provided to the comparator must be high enough to be within its operating range. Note that when the one-shot output ( -Q) is low, the voltage across R1 no-longer reflects the current through the motor winding. Therefore, the one-shot must be insensitive to the output of the comparator between the time it fires and the time it resets. Practical circuit designs using this approach involve some complexity to meet this constraint!
Selecting the value of R2 for the circuit shown in Figure 7 poses problems. If R2 is large, the current through the motor windings will decay quickly when the higher level control system turns off this motor winding, but when the winding is turned on, the current ripple will be large and the power lost in R2 will be significant. If R2 is small, this circuit will be very energy efficient but the current through the motor winding will decay only slowly when this winding is turned off, and this will reduce the cut off speed for the motor.
The peak power dissipated in R2 will be I2R2 during Toff and zero during Ton; thus, the average power dissipated in R2 when the motor winding is on will be: P2= I2R Toff / (Ton + Toff) Recall that the duty cycle D is defined as Ton / (Ton + Toff) and may be approximated as Vrunning / Vsupply. As a result, we can approximate the power dissipation as: P2= I2R2 (1 – Vrunning / Fsupply). Given the usual safety margins used in selecting power resistor wattages, a better approximation is not necessary.
When designing a control system based on pulse width modulation, note that the cutoff time for the one-shot determines Toff, and that this is fixed, determined by the timing network attached to the one-shot. Ideally, this should be set as follows: Toff = Lripple / Voff This presumes that the inductance L of the motor winding is known, that the acceptable magnitude of Iripple is known, and that Voff, the total reverse voltage in the current recirculation path, is known and fixed.
Note: This scheme leads to a variable chopping rate. As with the linear current limiters shown in Figure 3, the full supply voltage will be applied during the turn-on phase, and the chopping action only begins when the motor winding reaches the current limit set by Vref. This circuit will vary the chopping rate to compensate for changes in the back EMF of the motor winding, for example, those caused by rotor motion; in this regard, it offers the same quality of regulation as the linear current limiter.
The one- shot current regulator shown in Figure 7 can also be applied to an H-bridge regulator.
The encoded H-bridge is an excellent candidate for this application, as shown in Figure 8:

Unlike the circuit in Figure 7, this circuit does not provide design tradeoffs in the selection of the resistance in the current decay path; instead, it offers the same selection of decay paths as was available in the original circuit. If the X and Y control inputs are held in a running mode (01 Or 10), the current limiter will alternate between that running and slow decay modes, maximizing energy efficiency. When the time comes to turn off the current through the motor winding, the X and Y inputs may be set to 00, using fast decay mode to maximize the cutoff speed, while if the damping effect of dynamic braking is needed to control resonance, X and Y may be set to 11.
Note: The current recirculation path during dynamic braking does not pass through R1, and as a result, if the motor generates a large amount of power, burnt out components in the motor or controller are likely. This is unlikely to cause problems with stepper motors, but when dynamic braking is used with DC motors, the current limiter should be arranged to remain engaged while in braking mode!